С этой точки зрения представляет определенный интерес статья известного американского специалиста в области гидродинамики быстроходных судов Е. Р. Клемента, посвященная расчету сопротивления глиссирующего корпуса при оптимальном режиме глиссирования (опубликована в 1979 в журнале «International Shipbuilding Progress», том 26, № 295).
В 1963—1964 гг. при участии Клемента были выполнены испытания систематической серии моделей глиссирующих корпусов, известной как серия «62». Испытания проводились в опытовом бассейне имени Д. Тейлора, принадлежащем Научно-исследовательскому центру кораблестроения ВМС США. Описание указанных моделей и некоторые результаты их исследования были опубликованы ранее в сборнике (№ 66, 1977 г.), а также в книге И. Т. Егорова, М. М. Бунькова, Ю. М. Садовникова «Ходкость и мореходность глиссирующих судов», выпущенной в 1978 г. издательством «Судостроение».
В упомянутой выше новой статье Клемент представил сводный график буксировочных испытаний моделей серии «62», являющийся важным дополнением к ранее опубликованным материалам.
Как известно, смоченная поверхность большинства глиссирующих корпусов имеет форму, близкую к призматической, т. е. имеет почти постоянную ширину и килеватость при прямых линиях батоксов. Сопротивление при глиссировании корпуса такой формы является функцией нескольких переменных и может быть определено на основе результатов предварительно выполненных модельных испытаний или аналитическим расчетом.
Серия «62» включала пять моделей с различным удлинением, имевших одинаковую форму шпангоутных сечений и один угол килеватости 12,5°. Каждая модель серии была испытана при десяти различных водоизмещениях и положениях центра тяжести (ЦТ).
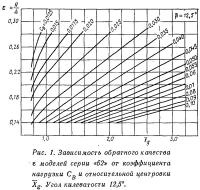
Результаты всех 50 испытаний на высоких скоростях, соответствующих устойчивому режиму глиссирования, были сведены в один общий график, приведенный на рис. 1. Этот график соответствует высокоскоростным режимам движения глиссирующих корпусов, имеющих широкий диапазон изменения относительной ширины, веса и положения ЦТ.
График построен в осях ε—Xg, где:
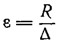
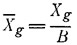
На графике нанесены кривые величины безразмерного сопротивления е в функции от относительной центровки Xg. Каждая кривая соответствует определенному постоянному значению коэффициента нагрузки
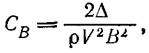
где Δ — весовое водоизмещение, т;
ρ — массовая плотность, кг·с2/м4 (равная 102 кг·с2/м4 для пресной воды и 104 кг·с2/м4 для соленой);
V — скорость хода, м/с;
В — ширина глиссирующей поверхности по скуле в плоскости ЦТ.
Промежуточные кривые сопротивления для любого сочетания указанных вариаций можно легко получить посредством интерполяции экспериментальных кривых.
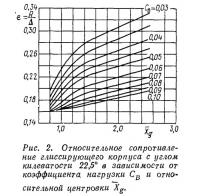
Строго говоря, использование графика ограничивается только областью, близкой к исследованной форме корпуса. Однако графики, подобные представленному на рис. 1, могут быть построены на основе модельных испытаний или путем расчета и для других величин угла килеватости. Например, сравнительно ограниченное число модельных испытаний специальных глиссирующих корпусов с обводами «глубокое V», имеющих продольные реданы, может быть использовано, чтобы построить аналогичный график и затем использовать его при вариациях проектных ситуаций для данной формы корпуса. В качестве примера на рис. 2 приведен такой график для призматической глиссирующей поверхности с углом килеватости 22,5°. Для построения графика использованы материалы Норвежского опытового бассейна, опубликованные П. Веренскольдом в 1970 г.
Применение графика рис. 1 можно показать на примере. Допустим, необходимо определить сопротивление глиссирующего корпуса, форма которого аналогична или близка форме корпуса серии «62». Известно, что корпус имеет водоизмещение Δ=1200 кг; ширина скулы в плоскости центра тяжести В=1,584 м; отстояние ЦТ от транца Xg=2,28 м. Катер должен развить скорость 45 км/ч (12,5 м/с).
Определяем относительную центровку:
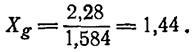
Считается, что при установившемся движении отстояния ЦТ и центра давления от транца одинаковы.
Рассчитывается коэффициент нагрузки для заданных характеристик глиссирования:
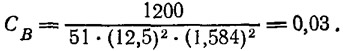
В соответствии с найденными Хg и Св по рис. 1 определяем обратное качество ε=0,2. Затем, умножая водоизмещение катера на полученную величину ε=0,2, получаем величину сопротивления R=240 кгс.
Кроме того, при помощи рис. 1 можно легко оценить влияние изменения центровки на сопротивление при широкой вариации ширины скулы в плане.
Допустим, в вышерассмотренном примере скорость, водоизмещение и ширина остались без изменения, а требуется определить эффект изменения продольного положения ЦТ. Поскольку коэффициент нагрузки остается постоянным, на соответствующей кривой сразу видно, что если ЦТ смешается в нос так, например, что Xg=1,6, сопротивление возрастает до 256 кг; а при_смещении ЦТ в корму, скажем, до Xg=1,1, сопротивление уменьшится приблизительно до 220 кг.
Указанная взаимосвязь между сопротивлением и положением ЦТ объясняет характерную особенность проектов многих быстроходных катеров, заключающуюся в расположении основных весов (двигателей и т. д.) как можно ближе к транцу. Однако, если продольная координата ЦТ будет слишком мала, вероятно появление неустойчивости глиссирования на высоких скоростях. Именно эта опасность ограничивает использование области графика, соответствующей максимальному гидродинамическому качеству.
При помощи рис. 1 можно также оценивать влияние изменения ширины при создании новых проектов. Уменьшение ширины вызывает увеличение коэффициента нагрузки, что, в свою очередь, будет приводить к снижению сопротивления, если при этом не увеличивать относительную центровку.
Стремление к использованию указанной взаимосвязи между шириной, положением ЦТ и сопротивлением прослеживается в большинстве проектов мореходных гоночных катеров. Как известно, установка продольных реданов на днище с повышенной килеватостью позволяет обеспечить глиссирование на большой скорости при уменьшенной ширине несущей поверхности корпуса. Переход на указанный режим движения должен сопровождаться смещением ЦТ в сторону транца, чтобы сохранить оптимальную относительную центровку при уменьшении ширины глиссирования. На ряде проектов это достигается за счет перекачки жидкого балласта или топлива из носовых цистерн в кормовые по мере набора скорости.
Вышеприведенные рассуждения показывают, что сопротивление типичных глиссирующих корпусов на высокой скорости может быть понижено или смещением ЦТ в корму, или уменьшением смоченной ширины. Главный эффект любой из этих двух мер заключается в уменьшении площади глиссирования.
Представляет очевидный интерес возможность определения того, насколько этот процесс может быть выполнен или, другими словами, какова оптимальная площадь глиссирующей поверхности, необходимая для поддержания данной массы катера на заданной скорости.
В этой связи представляет интерес тенденция изменения кривых сопротивления на рис. 1. Например, кривая для Св=0,03 (в расчетном примере она соответствует Δ=1200 кг, В=1,584 м и V=45 км/ч), указывает, что сопротивление будет продолжать уменьшаться, если ЦТ сдвигать к транцу ближе того минимального расстояния, которое представлено на графике (т. е. ЦТ смещается настолько близко к транцу, чтобы получить Xg<0,75). Однако такую тенденцию трудно реализовать на практике из-за появления продольной неустойчивости глиссирования. Нижнее ограничение Xg=0,75 на рис. 1, которое было получено при испытаниях моделей безреданных корпусов, соответствует минимальной величине, при которой модели могли быть испытаны без появления продольной неустойчивости.
Следовательно, чтобы спроектировать оптимальную несущую поверхность при минимальном сопротивлении и обеспечении устойчивости движения, необходимо изменить гидродинамическую компоновку глиссирующей поверхности, используя, например, продольные реданы.