Информация об изображении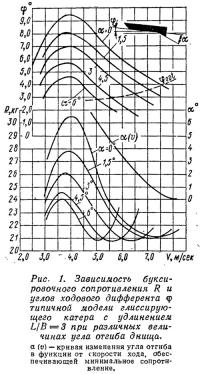
Рис. 1. Зависимость буксировочного сопротивления и углов ходового дифферента
Глиссирующие катера с малой относительной длиной (L/B≤3) в переходном режиме движения, как правило, имеют чрезмерный ходовой дифферент, значительно увеличивающий сопротивление воды. Отгиб днища вниз в кормовой части корпуса позволяет существенно уменьшить углы ходового дифферента и, следовательно, гидродинамическое сопротивление в переходном режиме (рис. 1). Однако с увеличением скорости и переходе на движение в режиме чистого глиссирования отгиб днища приводит к тому, что углы ходового дифферента оказываются меньше оптимального, который в зависимости от килеватости и формы днища в плане должен составлять 3,5—5°. Уменьшение дифферента приводит к резкому возрастанию смоченной поверхности днища и, следовательно, к увеличению сопротивления трения, которое на этом режиме играет уже преобладающую роль в полном гидродинамическом сопротивлении.

Рис. 1. Зависимость буксировочного сопротивления и углов ходового дифферента
Поскольку каждой скорости соответствует свое, определенное оптимальное значение угла дифферента, предпочтительнее использовать не фиксированный отгиб днища, а управляемые транцевые плиты, которые могут располагаться под наиболее выгодным для каждого режима движения углом атаки.
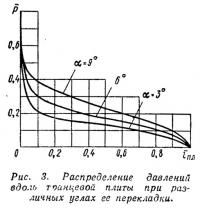
Принцип действия транцевых плит схематически показан на рис. 2. Изменение продольного момента при отклонении плиты обусловлено не только появлением дополнительной гидродинамической нормальной силы rп на самой плите, но и перераспределением давлений на днище. По мере приближения к транцу (на рисунке — точка В) поток жидкости, движущийся вдоль днища, подтормаживается, вследствие чего давление в этой части днища заметно повышается (для сравнения на том же рисунке пунктиром нанесена эпюра давлений на днище без транцевой плиты). Очевидно, что дополнительный гидродинамический момент, возникающий при перекладке транцевой плиты на некоторый угол и вычисляемый относительно транца, будет определяться разностью момента нормальной силы, развивающейся на плите, и момента дополнительных давлений на днище.
Гидродинамическая нормальная сила и ее шарнирный момент относительно оси поворота плиты могут быть рассчитаны теоретическим методом. Для упрощения вычислений размах днища B/Lсм предполагается большим, а жидкость — невесомой и невязкой. Это дает возможность свести исследование к решению плоской задачи о глиссировании ломаной пластины, состоящей из двух отрезков (рис. 2, а). Первый отрезок АВ длиной Lсм, равной смоченной длине катера, располагается под углом атаки φ по отношению к направлению движения.
Второй отрезок BD имеет длину lпл, равную длине плиты, и повернут относительно первого участка АВ на произвольный угол α. В результате решения, приведенного полностью в работе [1], получены зависимости, позволяющие рассчитывать распределение давлений вдоль участка BD, т. е. вдоль плиты (рис. 3), подъемную силу на плите и момент подъемной силы относительно точки В (шарнирный момент на плите) для различных сочетаний угла атаки днища φ, угла перекладки плиты α и относительной смоченной длины:
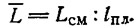
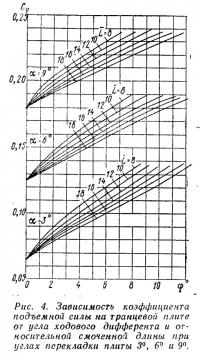
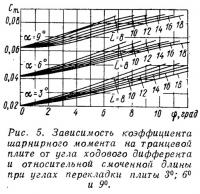
Значения коэффициентов подъемной силы на плите Сy и шарнирного момента Сm приведены на рис. 4 и 5 в зависимости от угла дифферента для относительных смоченных длин L=8÷18 и углов перекладки α=3°, 6° и 9°.
Подъемная сила и шарнирный момент, приходящиеся на единицу ширины транцевой плиты, определяются по формулам:
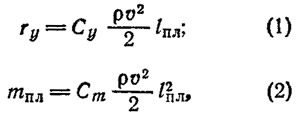
где ρ — плотность жидкости, кг/см2сек4;
υ — скорость хода, м/сек.
Значения коэффициентов Сy и Сm снимаются с графиков (рис. 4 и 5) в зависимости от угла дифферента, угла перекладки плиты и относительной смоченной длины. По известным значениям Сy и Сm можно найти также плечо шарнирного момента на плите или отстояние точки приложения подъемной силы от оси поворота:
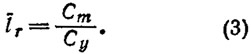
Сопоставляя значения Сm и Сy, приведенные на рис. 4 и 5, легко видеть, что подъемная сила на плите приложена на расстоянии ≈34% длины плиты от шарнира.
Решение задачи о глиссировании ломаной пластины бесконечного размаха, полученное в предположении отсутствия весомости жидкости, справедливо только для очень больших чисел Фруда:
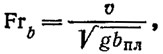
где υ — скорость движения, м/сек;
bпл — ширина плиты, м;
g = 9,81 м/сек2.
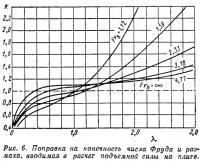
Реальные катера имеют совершенно определенный размах и движутся с конечными скоростями. Поэтому в формулы для расчета усилий на плите необходимо ввести поправку k(Frb; λ) на конечность числа Фруда и конечность размаха [2]:
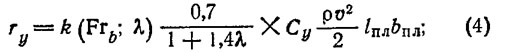
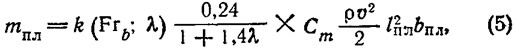
где k(Frb; λ) — поправка, определяемая по графику (рис. 6) в зависимости от числа Фруда и удлинения транцевой плиты:
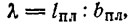
где lпл — длина, а bпл — ширина плиты, м.
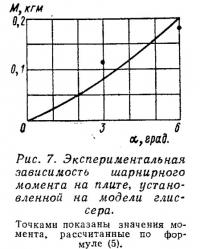
На рис. 7 показаны результаты измерений шарнирного момента на управляемой транцевой плите, установленной на модели глиссера, испытывавшейся в опытовом бассейне. Точками на графике нанесены значения момента, рассчитанные для соответствующих сочетаний угла перекладки, дифферента и относительной смоченной длины по формуле (5) с использованием графика (рис. 4). Расхождение найденных теоретически значений шарнирного момента с замеренными экспериментально не превышает 15%, что может считаться вполне удовлетворительным и позволяет с достаточной уверенностью использовать приведенные в статье формулы и графики для оценки гидродинамических характеристик управляемых транцевых плит.
Литература
- 1. Павленко А. С.. Соловей С. Б., К расчету сил, действующих на ломаную глиссирующую пластину, Труды НТО СП, вып. 168, 1971.
- 2. Эпштейн Л. А., Методы теории подобия и размерности в гидромеханике судна, «Судостроение», 1970.