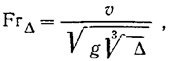Разработанный кандидатом технических наук М. М. Буньковым расчетный метод, на первый взгляд, кажется громоздким и сложным для практического применения. Однако благодаря тому, что приведены цифровые значения производных (они сведены в таблицу) расчет сводится к элементарным вычислениям.
Следует заметить, что наиболее достоверные результаты подобные расчеты дадут для сравнительно крупных катеров, так как относительная длина катеров длиной 4—10 м, составляющая L/B=2,25÷3,5, ниже значений испытанных М. М. Буньковым моделей.
Несмотря на то, что проектированием быстроходных катеров .занимаются более 50 лет, до настоящего времени отсутствовали надежные методы для расчета сопротивления воды их движению.
Для получения систематических данных по сопротивлению быстроходных катеров, движущихся с относительной скоростью1 FrΔ>2,5, автором была разработана и испытана в опытовом бассейне систематическая серия моделей остроскулых катеров (реданных и безреданных), а также катеров с комбинированными обводами (острая скула в корме и лекальные обводы в носу). Серия состояла из четырех групп моделей: группа А — модели с различной формой шпангоутов; группа Б — с остроскулыми безреданными обводами; группа В — с комбинированными обводами; группа Г — с реданными обводами.
На моделях варьировались следующие параметры:
а) форма шпангоутов — группа А;
б) коэффициент статической нагрузки:
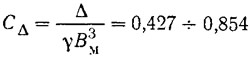
— для каждой модели;
в) относительная центровка, характеризуемая отстоянием центра тяжести от транца и выраженная в долях длины по скуле,
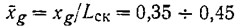
— для каждой модели;
г) относительная длина, т. е. отношение длины по скуле к ширине на миделе или на редане:
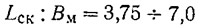
— группы Б и В;
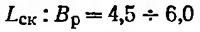
— группа Г;
д) угол внешней килеватости β на миделе (редане), представляющий собой угол между днищевой ветвью мидель-шпангоута (редана) и горизонтальной плоскостью:
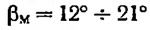
— группы Б и В;
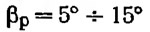
— группа Г;
е) угол внешней килеватости на транце:
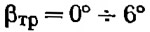
— группа Б;
ж) сужение кормовой оконечности, характеризуемое отношением ширины по транцу к ширине на миделе,
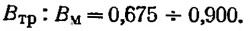
Обводы моделей группы А представлены на рис. 1. При изменении параметра СΔ ширина модели оставалась постоянной, а варьировалось водоизмещение в диапазоне от 75 до 150 кг.
При изменении LCK:ВМ в группах Б и В варьировалась длина модели (при неизменных сечениях по шпангоутам), в группе Г — ширина.
При изменении угла внешней килеватости на миделе линия скулы в плане, ширина на миделе, угол внешней килеватости на транце и сужение кормовой оконечности оставались неизменными.
Изменения сужения кормовой оконечности осуществлялись за счет ширины транца. При изменении угла внешней килеватости на транце форма скулы в плане и килевзтость на миделе сохранялись неизменными.
В процессе испытаний на каждой модели серии устанавливался брызгоогражаюший брус па длине от 0 до 12 теоретического шпангоута.
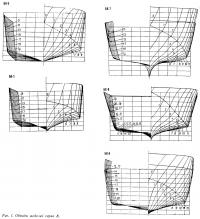
В результате испытаний получены зависимости (рис. 2) величины обратного качества (или удельного сопротивления):
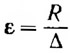
в диапазоне относительной скорости FrΔ = 1÷4,5.
Анализ результатов испытаний показывает, что наиболее существенное влияние па сопротивление R оказывают форма шпангоутов, коэффициент статической нагрузки, относительная центровка, относительная длина и угол внешней килеватости на миделе.
Оказалось возможным удельное сопротивление голого корпуса катера с заданной формой шпангоутов представить в безразмерной форме в виде:
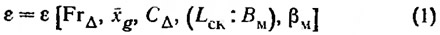
или, полагая Fr=const,
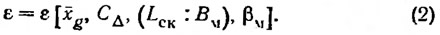
Анализ зависимости обратного качества в функции от одного параметра при постоянных прочих показал, что возможно представить обратное качество проектируемого катера аналитически в виде ряда Тейлора для функции многих переменных:

Значения производных получены для разных чисел Фруда путем обработки испытаний моделей систематической серии.
Производные:
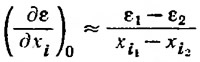
Информация об изображении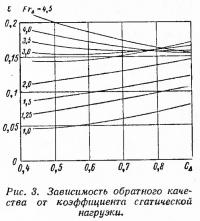
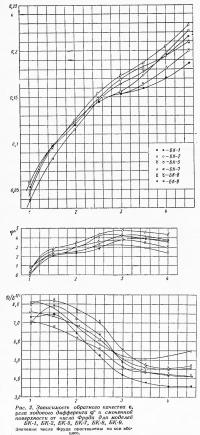
Рис. 3. Зависимость обратного качества от коэффициента статической нагрузки
учитывают относительное изменение величины обратного качества в зависимости от изменения рассматриваемого параметра xi и вычисляются по соответствующим графикам xi, xi o — значения соответствующих характеристик теоретического чертежа проектируемого и исходного катера. В качестве иллюстрации на рис. 3 представлена зависимость обратного качества в функции от коэффициента нагрузки СΔ при числе Фруда в качестве параметра для одной из моделей серии. Аналогичные зависимости были построены и для других параметров корпуса.

Рис. 3. Зависимость обратного качества от коэффициента статической нагрузки
Для повышения точности расчета во внимание принимаются производные второго порядка:
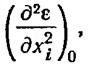
а в отдельных случаях, когда имеет место нелинейная зависимость ε от какого-либо параметра, необходимо учитывать и производную третьего порядка (например,
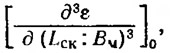
при Fr=1,5 и 2,0). В подавляющем большинстве случаев производные третьего порядка весьма малы и чаще даже равны нулю. Таким образом,
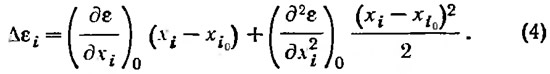
При этом следует учесть, что значение параметра xi для проектируемого катера должно лежать внутри области изменения этого же параметра на графиках, с помощью которых определяются приближенные значения величин частных производных, так как экстраполяция нежелательна.
Поправка Δεi учитывает изменение сопротивления за счет влияния одною какого-либо безразмерного параметра при данном числе Фруда, если считать остальные параметры неизменными. Но достаточно изменить один из каких-либо параметров корпуса, как ветчины первой и второй производных также претерпевают изменения. Для учета этого взаимного влияния необходимо определить также смешанные производные как второго, так и третьего порядков. Окончательно формула для определения обратного качества проектируемого катера приобретает следующий вид:
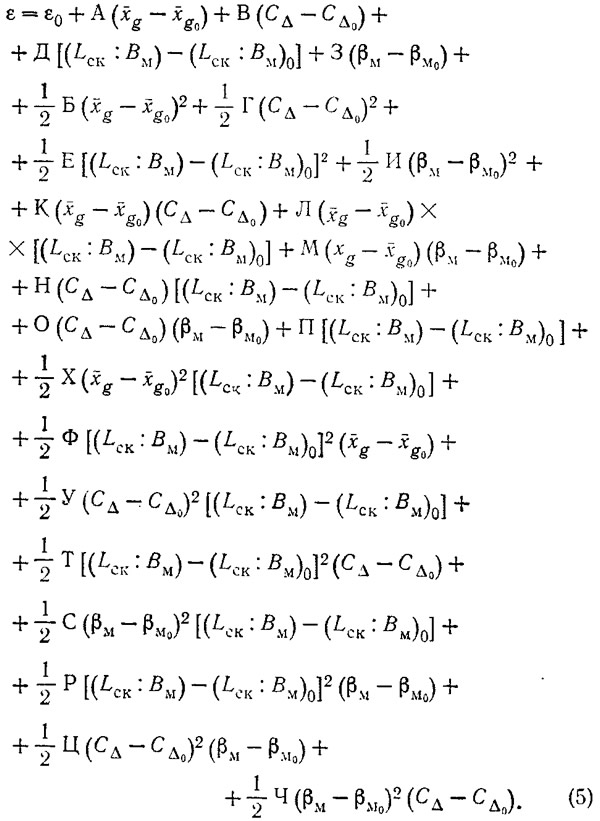
При определении значений производных в качестве исходных начальных параметров были приняты следующие параметры исходной модели группы Б:
Значения производных первого, второго и третьего порядков приведены в таблице. Исходя из этой таблицы и имея кривую удельного сопротивления прототипа в виде ε0=f(FrΔ), с помощью выражения (5) можно определить сопротивление голого корпуса проектируемого судна с произвольными параметрами корпуса и обводами, близкими к обводам моделей группы Б.
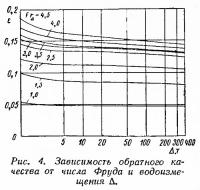
Приближенно указанный метод расчета может быть распространен и на быстроходные катера, имеющие форму шпангоутов моделей группы А. При этом в качестве исходной кривой удельного сопротивления ε0 могут быть использованы кривые, представленные на рис. 2. На этом же рисунке приведены кривые углов ходового дифферента и смоченной поверхности. При расчете сопротивления натурного судна кривые ε0=f(FrΔ) необходимо пересчитать на натуру по существующей методике пересчета. В качестве иллюстрации вышесказанного на рис. 4 представлена зависимость ε0=f(FrΔ, Δ), полученная при пересчете результатов испытаний голого корпуса модели 1. При указанном пересчете надбавка на шероховатость корпуса не учитывалась, так как она зависит от материала корпуса. Обычно надбавка на шероховатость для стальных сварных корпусов катеров составляет 0,4·10-3, для деревянных 0,1÷0.15·10-3.
Кроме того, при расчете сопротивления натурного катера необходимо учесть воздушное сопротивление и сопротивление выступающих частей (влияние воздушвого сопротивления при испытаниях исключалось установкой перед моделью аэродинамического щита). Для практических расчетов коэффициента воздушного сопротивления натурных катеров можно использовать следующую приближенную формулу:

где SM — проекция надводной части судна на плоскость миделя:
Ω — смоченная поверхность судна.
Сопротивление выступающих частей определяется по испытанию модели с установленными на ней рулями и валами с кронштейнами. Для практических целей можно сопротивление выступающих частей пересчитывать пропорционально кубу масштаба. В случае, когда отсутствуют данные модельных испытаний, полное сопротивление выступающих частей может быть приближенно рассчитано по элементам. Определяется сопротивление изолированных кронштейнов, рулей, валов по данным испытаний в опытовом бассейне и в аэродинамических трубах, а затем вносятся необходимые поправки на возможную интерференцию.
Рассчитав сопротивление голого корпуса по предлагаемому методу и определив воздушное сопротивление, сопротивление выступающих частей и от шероховатости корпуса, получим полное буксировочное сопротивление натурного катера.
Литература
- Я. И. Войткунекий, Сопротивление воды. Издательство «Судостроение», 1964.
- М. М. Буньков, Ю. М. Садовников, Сопротивление и пропульсивные качества быстроходных катеров, «Судостроение», № 7. 1958.
Примечания
1. Число Фруда по водоизмещению: