Задачей сегодняшнего дня в отечественном буерном спорте, на наш взгляд, является штурм 200-километрового рубежа. Сигнал к началу этого штурма подал таллинский буерист В. Гирс. Как уже сообщалось в сборнике, в марте 1966 г. на аэродинамическом буере класса 12 м2 он показал рекордную скорость около 124,5 км/час. Можно ли преодолеть остальные 75,5 км/час? На самом деле, может ли парус (будь то парус в его классическом виде или крыло) хотя бы в идеальных условиях обеспечить движение яхты (буера) с такой огромной скоростью?
На последний вопрос дал ответ Ю. С. Крючков [1]. Он показал, что предельно возможную скорость хода под парусом развивает воображаемое идеальное судно, которое не испытывает сопротивления воды, но вместе с тем обладает бесконечно большим сопротивлением боковому сносу (дрейфу). Модель такого судна легко себе представить, например, в виде некоторого крыла, движущегося в установившемся потоке воздуха, высоко над поверхностью воды, вдоль бесконечно тонкой и абсолютно жесткой нити. Центр поддержания крыла на этой воображаемой нити совпадает с центром давления, а поэтому движение осуществляется устойчиво — без крена и дифферента.
Скорость хода идеального парусного судна υ (м/сек) может быть определена [1] по формуле:
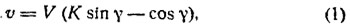
где V — скорость истинного ветра, м/сек; γ — курс судна относительно истинного ветра; К — аэродинамическое качество судна.
Если для простоты расчетов полагать, что идеальное судно идет курсом галфвинд (γ=90°), эта формула примет вид:
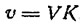
Допустим, что парус судна имеет профиль МУНК-1, обладающий [2] аэродинамическим качеством К=23,6 при удлинении λ=6. Теперь нетрудно подсчитать, что для достижения скорости хода 200 км/час (55,5 м/сек) идеальному парусному судну потребуется очень нет большой силы ветер, дующий со скоростью:
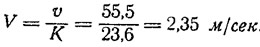
Однако возвратимся от идеальных к действительным условиям работы крыла на буере, коньки которого при движении испытывают некоторое сопротивление льда, а обычно используемый способ несения паруса вызывает действие кренящего момента. Развивая основные идеи, высказанные в работах [1], и рассматривая реальное парусное судно как аэрогидродинамический комплекс системы корпус — парус — поток воздуха, автор настоящей статьи получил следующую зависимость скорости хода буера от основных его конструктивных параметров, скорости истинного ветра и курса относительно истинного ветра:
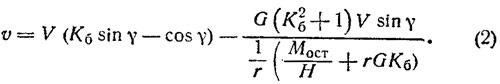
Здесь учитываются:
G — вес буера, кг;
Мост — момент поперечной остойчивости, необходимый для несения паруса при движении буера со скоростью υ и заданным углом крена φ, кгм;
Н — возвышение центра давления паруса ЦД над центром поддержания буера ЦП, т. е. над поверхностью льда, м;
Кб — аэродинамическое качество буера;
r=R/G — удельное сопротивление, где R — сопротивление, которое оказывает конькам лед при движении буера со скоростью υ.
Приведенная основная формула (2) и ряд промежуточных сопутствующих ей зависимостей могут быть использованы для проведения аэродинамического расчета буеров.
Используя формулу (2), можно установить, что рекордный буер для достижения скорости хода 200 км/час на курсе галфвинд при выше принятых допущениях и скорости ветра υ=10 м/сек должен иметь, например, следующие характеристики: G=650 кг; Мост=925 кгм; H=3,7 м; 1/r=33; Kб=10.
Покажем теперь, что такие конструктивные характеристики буера могут быть достигнуты в действительности.
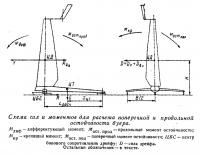
Наибольший момент поперечной остойчивости, которым располагает буер, идущий без крена, может быть рассчитан по формуле Н. В. Григорьева [3]:
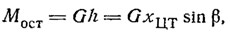
где h — плечо поперечной остойчивости буера при накренении его вокруг оси l-l, проходящей через центры качания подветренного бортового и рулевого коньков; величина h в плоскости рисунка определяется длиной отрезка перпендикуляра, опущенного из центра тяжести ЦТ буера на ось l-l; β — конструктивный угол, составляемый осью l-l и ДП буера.
Приняв β=23°45' (по прототипу — буеру № 80 В. Гирса), можно вычислить необходимое наименьшее отстояние центра тяжести ЦТ буера от баллера рулевого конька из условия обеспечения движения без крена:
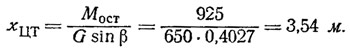
При длине нашего рекордного буера Lрасч=6,34 м величина xЦТ=3,54 м вполне осуществима и приемлема по всем иным соображениям, например, по условиям устойчивости на курсе.
Н. В. Григорьев рекомендует [3] вычислять силу трения коньков о лед в условиях хорошей дороги по формуле R=0,03G. Тогда удельное сопротивление действительно составит г=1/33.
Предварительный расчет показывает, что достаточно установить крыло площадью S=4 м2, имеющее коэффициент подъемной силы Сy=0,3 на расчетном режиме. Используя одну из выведенных нами промежуточных зависимостей, можно убедиться, что заданная скорость хода будет при этом достигнута:
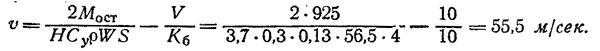
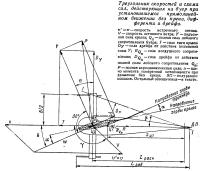
Здесь величина массовой плотности воздуха ρ=0,13 кг•сек2/м4 принята для температуры около 0°С, а скорость вымпельного ветра W для курса галфвинд вычислена из треугольника скоростей:
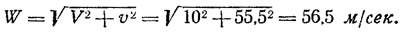
Заметим, что курс буера относительно вымпельного ветра Θ=10,2°.
Под расчетным режимом работы крыла понимается его установившееся движение под наивыгоднейшим углом атаки αнаив к набегающему потоку W; при этом, как известно, углу αнаив будет соответствовать и максимальное значение аэродинамического качества крыла К.
Принятое в расчете сравнительно низкое значение Сy=0,3 при работе крыла на αнаив обеспечивает, например, тонкий симметричный профиль МУНК-1 при λ=6, о котором уже упоминалось выше. Большим его достоинством, помимо высокого значения К, является относительно небольшое перемещение ЦД при изменении угла атаки, что очень важно для предотвращения штопора при маневрах на больших скоростях.
Из выражения:
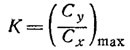
можно определить расчетное значение Cx крыла: Cx=0,0127.
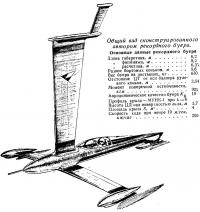
Предварительный расчет Кб показал, что рекордный буер должен представлять собою нечто, соответствующее в аэродинамическом отношении наиболее совершенным современным планерам. Конечно, не может быть и речи об открытом стоячем и бегучем такелаже. Необходимо ликвидировать или закрыть все мелкие наружные детали и применить наивыгоднейшие формы для крупных. Фюзеляж должен иметь минимальную площадь поперечного сечения овальной формы и плавные обводы. Хорошо обтекаемый фонарь, вписывающийся в обводы фюзеляжа, обусловливает почти лежачее положение рулевого в кокпите.
Для снижения сопротивления трения большое значение имеет качество отделки поверхностей всех деталей и крыла вплоть до полировки их специальными пастами непосредственно перед стартом.
Проиллюстрируем сказанное примером.
В авиации при расчете летательных аппаратов используется формула:
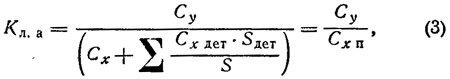
где Су, Сх, S — коэффициенты и площадь изолированного несущего крыла, работающего на заданном угле атаки;
Сх дет, Sдет — коэффициент лобового сопротивления и воздушный мидель (площадь поперечного сечения) некоторой несущей, «вредной» детали (фюзеляжа, оперения, расчалок и т. д);
Сх п — коэффициент полной силы лобового сопротивления;
В=1,05÷1,1 — эмпирический коэффициент, учитывающий интерференцию деталей и ряд мелких сопротивлений.
Приведенная формула (3) может быть использована также и при расчете яхт и, в частности, нашего буера.
Для фюзеляжа, имеющего овальное поперечное сечение высотой 0,65 и шириной 0,50 м, площадь воздушного миделя Sдет=0,32, а Сх дет=0,1 (по результатам продувок аналогичных фюзеляжей планеров при угле атаки Θ=10,2°, равном курсу буера относительно вымпельного ветра); Сy фюзеляжа по малости во внимание не принимается.
Для поперечного бруса длиной 5,6 м, имеющего также овальное поперечное сечение 0,45X0,09 м, Sдет=0,5 м2, а Сх дет=0,063.
Значения коэффициентов крыла уже приводились выше. Учитывая влияние выступающих деталей и интерференцию при помощи коэффициента B=1,05, подсчитаем значения Kб для нашего рекордного буера:
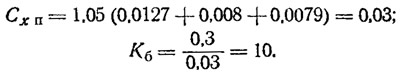
Установка концевых шайб по краям крыла повысит эффективное удлинение λэ и тем самым обеспечит некоторый запас Кб сверх величины, полученной по расчету.
Обтекаемый поперечный брус на большой скорости движения может работать как несущее крыло, поэтому необходимо принять меры для предотвращения «взлета» буера и его опрокидывания. Для этого можно, например, оборудовать поперечный брус управляемыми закрылками, при отклонении которых вверх создается отрицательная подъемная сила («аэродинамический балласт»).
Как уже отмечалось, движение буера с расчетной скоростью 200 км/час возможно на режиме, который определяется углом атаки αнаив. Поддержание расчетного режима движения в пределах узкой зоны наивыгоднейших углов атаки предлагается осуществлять специальным вспомогательным крылом-триммером, работающим в потоке вымпельного ветра W. Рулевой при помощи специальной проводки отклоняет триммер относительно хорды крыла на угол α, равный αнаив расчетного режима движения, а триммер, в свою очередь, выводит крыло на угол атаки αнаив и поддерживает заданный режим движения. Отклонение триммера на некоторый угол α, больший чем αнаив, обеспечивает движение буера в режиме меньшего К, т. е. в режиме с меньшей установившейся скоростью.
При неотклоненном триммере крыло устанавливается в положение левентик, и буер останавливается. Отклонение триммера на угол α, превышающий αкрит, нецелесообразно в связи с резким ухудшением условий обтекания крыла и крайне малым К.
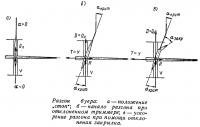
Самостоятельный разгон буера возможен только в том случае, если сила тяги крыла Т превышает силу сопротивления R. Рассмотрим — см. рис. а — частный случай разгона рекордного буера на курсе галфвинд из положения «стоп» (буер стронут с места).
Сила трения коньков о лед на малых скоростях движения:
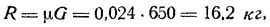
где μ — коэффициент трения коньков в условиях чистого гладкого льда [3].
Заметим, что в начальный момент движения полная сила лобового сопротивления Qп проявляет себя как сила дрейфа D, а подъемная сила Y работает полностью как сила тяги Т. Для получения наибольшего значения силы тяги Т=Y необходимо обеспечить с помощью триммера работу крыла на угле атаки, близком к αкрит, что обеспечивает наибольшую возможную для принятого профиля величину Сy max=0,805.
Вычислим силу тяги в начале разгона буера (рис. б):
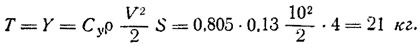
Под влиянием избыточной силы Т — R = 21—16,2 = 4,8 кг буер приобретает ускорение и начнет увеличивать скорость хода. Постепенное уменьшение угла отклонения триммера будет вызывать увеличение Кб, что и обеспечит дальнейший разгон.
Задача сокращения времени разгона буера требует более тщательного рассмотрения, однако укажем, что, например, оборудование крыла управляемым закрылком (рис. в) может повысить максимальное значение Сy до 1,2, что в свою очередь увеличит Т в начальный период разгона до величины Т=Y=31,2 кг. По мере разгона буера закрылок должен возвращаться в исходное неотклоненное положение.
Для нормального движения буера по курсу сила дрейфа не должна превышать 0,4÷0,6 G [3]. В нашем случае это условие выполняется, так как:
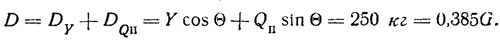
В заключение добавим, что вовсе не нужно рисковать жизнью при ураганном ветре, чтобы побить существующий рекорд скорости. Необходимо принять дополнительный балласт 130 кг в наветренный обтекатель поперечного бруса и дождаться ветра со скоростью 12 м/сек. Ожидаемая при таких условиях скорость хода 260 км/час, на наш взгляд, вполне реальна.
Литература
- 1. Ю. С. Крючков, «Может ли парусное судно идти быстрее ветра?», «Судостроение», № 6, 1961; «40 узлов под парусами», «Катера и яхты», выл. 14.
- 2. А. С. Кравец, Характеристики авиационных профилей, Оборонгиз, 1939.
- 3. Н. В. Григорьев, Вопросы теории буера с жестким крылом, «Катера и яхты», вып. 5.