Без знания остойчивости яхты трудно рационально спроектировать ее парусное вооружение, оценить ходкость, определить рабочую площадь парусности для различной силы ветра, рассчитать нагрузки, возникающие в рангоуте и такелаже, и решить целый ряд других задач. Поэтому важно уже на начальной стадии разработки проекта яхты иметь представление об остойчивости создаваемого судна.
Расчет остойчивости для парусной яхты включает решение двух основных задач:
- построение диаграммы восстанавливающих моментов и
- расчет величин кренящих моментов, возникающих под действием внешних сил.
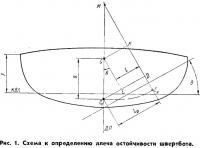
Напомним, что плечом статической остойчивости называется перпендикуляр, опущенный в плоскости наклонения из центра тяжести судна на линию действия силы плавучести в накрененном положении. Так, на рис. 1 плечом статической остойчивости является отрезок GK.
Из этого рисунка видно также, что:
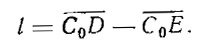
Отрезок C0D характеризует смещение центра величины при крене в сторону наклонения. Его величина зависит от обводов судна и поэтому его принято называть плечом остойчивости формы lф.
Отрезок C0 = αsinθ из прямоугольного треугольника GC0E; α = C0G — возвышение центра тяжести над центром величины при крене, равном нулю.
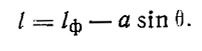
Таким образом, при известном положении центра тяжести G и центре величины С0 в прямом положении для расчета плеча статической остойчивости необходимо определить плечи остойчивости формы. Последнее для данных углов крена яхты, как мы уже отметили, зависит от обводов судна.
Для определения плеча остойчивости формы иногда применяется метод Кэмпфа, сущность которого сводится к плоскому моделированию погруженной при данном угле крена части корпуса.
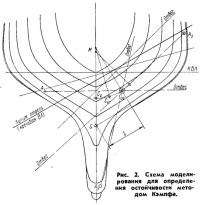
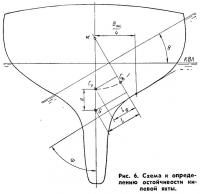
Для расчета остойчивости этим методом необходимо вычертить теоретические шпангоуты яхты на оба борта, вырезать их из плотной бумаги и склеить вместе. Таким образом, получается как бы сплюснутая по длине модель яхты (рис. 2). Таких моделей должно быть изготовлено столько, сколько углов крена подлежит расчету. Клеить надо аккуратно, совмещая пересечение ДП и КВЛ на одной оси для всех шпангоутов. Клей надо наносить тонким слоем. Следует помнить, что при этом методе определяется центр тяжести склеенной модели, поэтому следует избегать неравномерного нанесения клея. Когда все модели высохнут, первую модель (при угле крена θ=0°) аккуратно разрезают по КВЛ и нижнюю часть кладут на чашку точных аптекарских весов.
Вторую модель разрезают по намеченной на глаз наклонной линии, проходящей заведомо выше, но параллельно креновой ватерлинии при θ=15°. Нижнюю часть второй модели также кладут на весы, а затем подрезают ее — все время параллельно креновой ватерлинии — до тех пор, пока ее вес не сравняется с весом исходной модели. Нетрудно показать, что если число шпангоутов достаточно велико (не менее 10), то полученная линия отреза и будет креновой ватерлинией для данного угла крена.
Далее остается определить положение центра тяжести модели. Проще всего это сделать, подвешивая ее последовательно за 2—3 точки (например, точки А1, А2, А3) и отмечая положения отвесов из этих точек. Пересечение отвесов и даст нам положение центра тяжести модели, т. е. искомое положение центра величины яхты при крене. Повторяя эту процедуру нужное число раз и перекалывая положение ЦВ на чертеж с обозначенным ЦТ яхты, получим положения ЦВ и плечи статической остойчивости l, по которым можно построить диаграмму остойчивости.
Достоинствами этого метода являются его наглядность и простота. Точность его, по сравнению с аналитическим методом, как показывают параллельные расчеты, вполне удовлетворительна. Однако его использование связано с довольно большими затратами времени.
Ниже излагается обеспечивающий достаточную для практики точность метод быстрого приближенного расчета остойчивости парусных яхт, разработанный автором. Сущность метода — в использовании простой закономерности, заключающейся в том, что для геометрически подобных корпусов плечи их остойчивости формы lф пропорциональны поперечным линейным размерам, в частности — ширине В или ширине по КВЛ BWL.
Если бы все корпуса яхт были геометрически подобными, то по результатам расчета одного корпуса можно было бы легко рассчитать остойчивость любого подобного корпуса, полагая, что отношения lф/В для всех корпусов равны. Однако на положение ЦВ при крене и, таким образом, на величину плеча остойчивости формы оказывают влияние многие геометрические характеристики корпуса, например:
- килеватость корпуса, определяемая углом ки-леватости ф и характеризуемая также отношением ширины по КВЛ к осадке (BWL/T);
- полнота обводов, характеризуемая коэффициентом общей полноты δ;
- полнота ватерлинии, характеризуемая коэффициентом полноты ватерлинии α;
- развал бортов, характеризуемый отношением максимальной ширины яхты к ширине по КВЛ (B/BWL);
- относительная высота борта, характеризуемая отношением высоты борта к ширине или к ширине по КВЛ (F/B).
Установлено, что для швертботов определяющими параметрами геометрического подобия остойчивости являются:
— относительная высота борта:
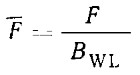
— относительное углубление BWL/T.
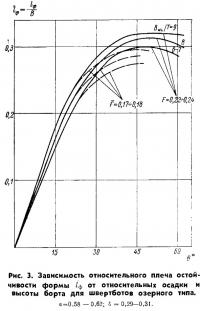
На рис. 3 показана статистическая зависимость относительного плеча остойчивости формы lф — lф/В от угла крена θ для озерных швертботов, подобных швертботам классов «М», «Т», «Финн», «Летучий голландец», «Ерш». Поскольку обрабатывались результаты расчетов вполне определенных швертботов, приведенные зависимости справедливы лишь веденные на рис. 3, можно применять для расчета остойчивости швертботов с относительной высотой борта F = 0,17÷0,13 и 0,22÷0,24, попадающих в следующие интервалы коэффициентов полноты:
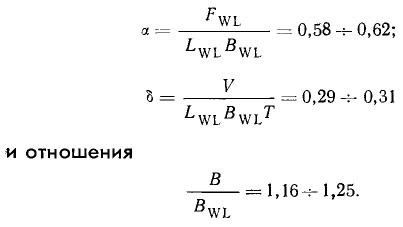
В указанные пределы попадает подавляющее большинство швертботов нормальных обводов и соотношений главных размерений.
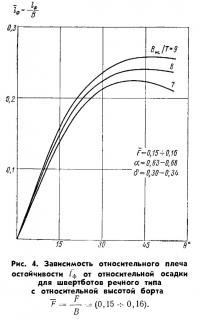
На рис. 4 показаны аналогичные характеристики для низкобортных швертботов (типа «Р2» и «РЗ»). Пределы применимости указаны на графике.
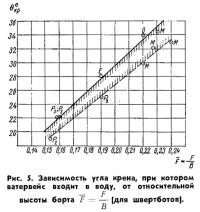
Угол крена, при котором палуба у миделя входит в воду (а этот крен обычно свидетельствует, что надо брать рифы), также довольно просто определить, пользуясь теми же статистическими данными. На рис. 5 показана эмпирическая зависимость указанного угла крена от относительной высоты борта F для швертботов. Как видно, крен θкр может быть определен с точностью ±1÷1,5°.
Аналогичное исследование остойчивости было проведено и для килевых яхт. При этом достаточно объективными критериями геометрического подобия для расчета плеча остойчивости формы оказались:
- ψ — угол килеватости, взятый по касательной к контуру мидель-шпангоута на расстоянии 1/4 BWL от ДП (рис. 6);
- F — относительная высота борта, в отличие от швертботов, отнесенная к ширине по КВЛ.
По приведенным в графиках данным можно легко рассчитать плечи и моменты остойчивости по формулам:
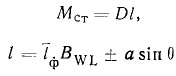
В этой формуле положительное а означает, что ЦТ находится ниже ЦВ, а отрицательное а принимается в случае, если ЦТ яхты расположен выше ЦВ.
Как и для швертботов, для килевых яхт может быть дана статистическая зависимость угла крена θкр, при котором ватервейс у миделя входит в воду (рис. 8).
Ошибка в определении плеча остойчивости указанным методом не превышает 3—6%, что обеспечивает достаточную точность расчетов. Естественно, что положения центра тяжести и центра величины яхты должны быть определены, по крайней мере, с не меньшей точностью.
Для примера приведем расчет остойчивости килевой яхты «Лоцман», чертежи которой опубликованы в первом выпуске сборника «Катера и яхты».
Напомним основные данные яхты: длина по КВЛ 5,28 м; длина наибольшая 6,765 м; ширина наибольшая 2,12 м; ширина по КВЛ 1,86 м; водоизмещение 1420 кг.
Определим ее геометрические характеристики, необходимые для расчета остойчивости:
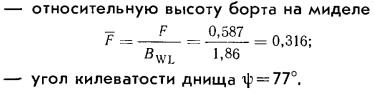
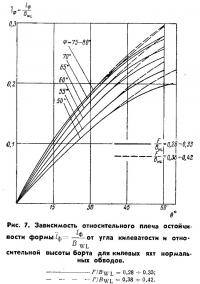
Расчет производится по графику (рис. 7) для килевых яхт, то кривой lф = f(θ) для угла килеватости 75—80° и F = 0,28÷0,33. Поскольку точные положения ЦВ при нулевом крене и ЦТ для яхты «Лоцман» нам неизвестны, для примера задаемся следующими координатами: ЦТ находится на высоте 50 мм над КВЛ, а ЦВ — на 120 мм под КВЛ. Таким образом α = 0,17 м.
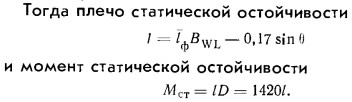
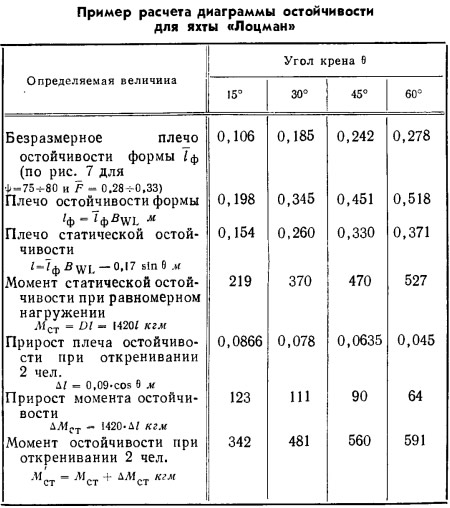
Таблица 1
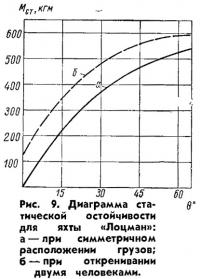
Данные расчета сведены в табл. 1, а диаграмма статической остойчивости изображена на рис. 9.
Для малых яхт большое значение имеет открени-вающий момент экипажа. Рассчитанная нами диаграмма остойчивости действительна для симметричного расположения грузов относительно ДП. При смещении части нагрузки ΔD на величину Δу к наветренному борту ЦТ яхты сместится на ветер на величину:
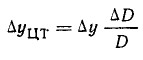
Если при этом та же часть нагрузки сместится еще и по вертикали на величину Δz, то вертикальное перемещение ЦТ будет:
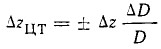
Знак «плюс» относится к перемещению этой части груза вниз, а знак «минус» — вверх. Тогда увеличение плеча статической остойчивости:
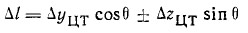
Предположим, что (вернемся к нашему примеру) два члена экипажа (ΔD = 160 кг) откренивают яхту, переместившись по горизонтали (Δz = 0) на наветренные банки, причем Δy = 0,8 м. Тогда:
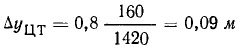
Соответствующие изменения плеч и моментов статической остойчивости будут равны:

Результаты расчета даны в табл. 1. Аналогичным образом можно рассчитать диаграмму остойчивости для любого случая перемещения грузов.
Как видно из примера, для таких маленьких яхт, как «Лоцман», откренивающий момент экипажа имеет очень большое значение для увеличения остойчивости.
Расчет кренящих моментов, возникающих под действием ветра на паруса, является темой отдельной статьи. Здесь же уместно сделать ряд замечаний по выполнению этого расчета.
Почти во всех книгах по парусному спорту и в курсах теории корабля для кренящего момента от действия ветра на паруса приводятся зависимости:
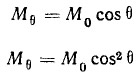
где Мθ — кренящий момент при угле крена θ=0°.
Эти зависимости более или менее справедливы для яхты, идущей курсом галфвинд с парусом, стоящим в ДП, или для старинных парусников, которые не плавали с креном 40—50°. Для расчета остойчивости последних принимались колоссальные запасы по кренящим моментам, что не требовало использования более точной формулы. Однако сравнительные расчеты и ходовые испытания яхт показывают, что эти зависимости дают завышенные значения кренящих моментов. Практически отмечается существенно более быстрое падение кренящего момента с увеличением угла крена.
Более или менее достоверные экспериментальные данные по зависимости кренящего момента от угла крена, полученные при ходовых испытаниях яхт, имеются в работе Дэвидсона [2]. Согласно этим данным сила дрейфа, вызывающая крен яхты, в зависимости от угла крена изменяется для яхты с вооружением бермудский шлюп примерно так, как показано в табл. 2.

Таблица 2
Данные, полученные Дэвидсоном, в большой степени соответствуют явлениям, происходящим при обтекании парусов потоком воздуха при увеличении угла крена.
Довольно близкие к действительности результаты дает расчет кренящих моментов по формуле:
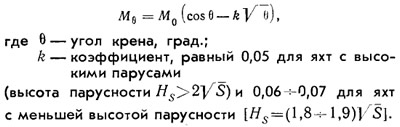
Литература
1. Н. В. Григорьев, Б. Б. Лобач-Жученко, Парусные гонки, «Физкультура и спорт», 1959.
2. К. S. М. Davidson, Some experimental studies of the Sailing Yachts, "Transactions of the Society of Naval Architects and Marine Engineers", 1937.
3. Ч. Mapxай, Теория плавания под парусами, «Физкультура и спорт», 1963.